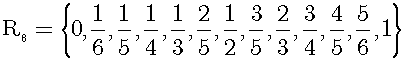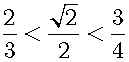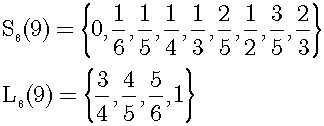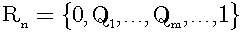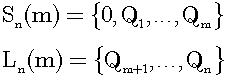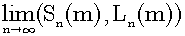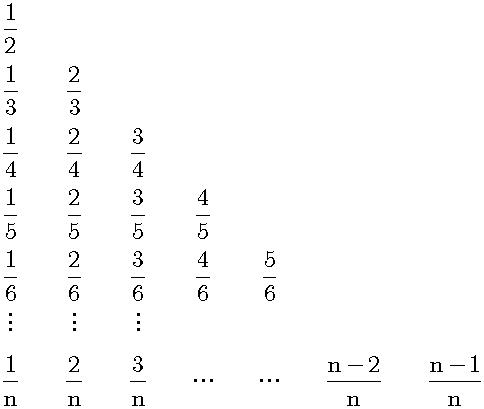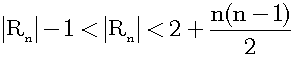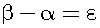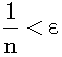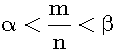Counting Real Numbers


Summary


Consider two different real numbers. The difference of them is ε. No matter how small ε is, there exists a natural number n such that: 1/n<ε. Then, there must be a rational number between two real numbers. Therefore, real numbers can be put into one-to-one correspondence with rational numbers.

The Cut of the Finite Set of Rational Numbers


    While Cantor claimed that real numbers in the interval [0,1] are uncountable, there is no attempt to count them before now. It is very difficult to count real numbers directly. However, Dedekind defined a real number as  a Dedekind cut. Then, we shall attempt to count Dedekind cuts. To achieve this goal, we shall count them step by step. First, we arrange all rational numbers with denominator not greater than 6 in the interval [0,1] in ascending order:
 
 
R6 represents the set of all rational numbers with denominator not greater than 6 in the interval [0,1]. Elements of R6 are only irreducible fractions. Then, we can sandwich an arbitrary real number in the interval [0,1] between two neighboring elements of R6. For example, √2/2 is between 2/3 and 3/4:
 
 
Thus, the real number √2/2 divide R6 into S6(9) and L6(9):
 
 
2/3 is 9th element of R6 in ascending order. The former set S6(9) contains elements of R6 not greater than 2/3. The latter set L6(9) contains elements of R6 greater than 2/3. Next, Rn represents the set of all rational numbers with denominator not greater than n in the interval [0,1] and Qm represents the m-th element of Rn in ascending order:
 

Consider an arbitrary real number α in the interval [0,1]. If α lies between Qm and Qm+1, then α divides Rn into Sn(m) and Ln(m):


We shall call this division of Rn the cut of Rn and write (Sn(m), Ln(m)). As n increases, then the cut of Rn approaches α:


The limit of (Sn(m), Ln(m)) equals the Dedekind cut defining α. As n increases, then the cut of Rn approaches the Dedekind cut. We can approximate the Dedekind cut by the cut of Rn as accurate as we want. Therefore, we can define the Dedekind cut as the limit of the cut of Rn without resort to geometric images.

Counting Cuts of the Finite Set of Rational Numbers 


    Next, we shall allow to overlap and list all fractions in the interval (0,1):



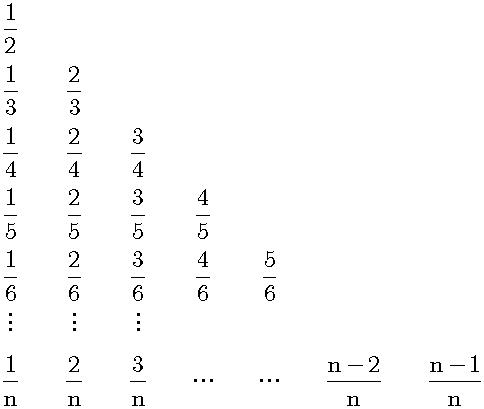Table 1


Table 1 contains all possible fractions with denominator not greater than n in the interval (0,1). The number of them is n(n-1)/2. On the other hand, Rn contains the simplest forms of these fractions and 0 and 1. The number of all elements of Rn is |Rn|. Then, if n is greater than 3, |Rn| is less than 2+n(n-1)/2: 


No matter how large n is, 2+n(n-1)/2 is a natural number. Obviously, |Rn| is a natural number and the number of cuts of Rn is |Rn|-1.Then, cuts of Rn are countable.

More Abstract Proof


    Consider a real number α and the larger real number β, and then β minus α equals ε: 


According to the axiom of Archimedes, no matter how small ε is, there exists a natural number n such that:


Then, there exists an integer m such that:


On the other hand, if there is no rational number between the two real numbers, then the difference between two numbers is zero. That is to say, they are the same number. Inevitably, there must be a rational number between two different real numbers. In other words, an arbitrary real number is sandwiched between two rational numbers. This means that real numbers can be put into one-to-one correspondence with rational numbers. Consequently, real numbers are countable.

Table of Contents